Sin resumen de edición |
Sin resumen de edición |
||
| (No se muestran 21 ediciones intermedias de 3 usuarios) | |||
| Línea 1: | Línea 1: | ||
| + | [[Imagen:Limit.png|right|thumb|200px|Límite]] |
||
| − | Siendo <math>y=f(x)</math> una función real de variable real, es decir: |
+ | Siendo <math>y=f(x)</math> una [[función]] real de variable real, es decir: |
:<math>f:\mathbb{R}\to \mathbb{R}</math> |
:<math>f:\mathbb{R}\to \mathbb{R}</math> |
||
| Línea 8: | Línea 9: | ||
Simbólicamente: |
Simbólicamente: |
||
| − | <math>\lim_{x \to a}f(x) = |
+ | <math>\lim_{x \to a}f(x) = l \iff \forall \quad \varepsilon > 0 \quad \exists \quad \delta ( \varepsilon) >0\quad /\quad si \quad 0<|x-a|< \delta \to |f(x)-l|< \varepsilon</math> |
Es decir, para todo epsilon mayor que 0 existe un delta que depende de epsilon y es mayor que cero, tal que, si los valores de "x" distan de "a" una cantidad menor que delta y son distintos de "a", entonces los correspondientes valores de f(x) distan de "l" una cantidad menor que epsilon. |
Es decir, para todo epsilon mayor que 0 existe un delta que depende de epsilon y es mayor que cero, tal que, si los valores de "x" distan de "a" una cantidad menor que delta y son distintos de "a", entonces los correspondientes valores de f(x) distan de "l" una cantidad menor que epsilon. |
||
| + | |||
| + | Si obervamos <math>0<|x-a|< \delta</math> podemos ver que a "a" no se le exige la condición ya que en los límites sólo se estudia el comportamiento en las ''proximidades''. |
||
| + | |||
| + | == Propiedades de los límites == |
||
| + | *El límite de una función en un punto si existe , es único y es igual a los límites laterales. |
||
| + | *Si una función tiene limite distinto de cero en un punto entonces existe un entorno del punto en el que los valores que toma f tienen el mismo signo que el límite . |
||
| + | *<math>\lim_{x\to a}f+g=\lim_{x\to a}f + \lim_{x\to a}g</math> |
||
| + | *<math>\lim_{x\to a}f\cdot g=\lim_{x\to a}f \cdot \lim_{x\to a}g</math> |
||
| + | *<math>\lim_{x\to a}k\cdot f=k\cdot \lim_{x\to a}f</math> Si <math>k</math> es una constante. |
||
| + | *<math>\lim_{x\to a}\frac{f}{g}=\frac{\lim_{x\to a}f}{\lim_{x\to a}g}</math> si <math>\lim_{x\to a}g\ne 0</math> |
||
| + | |||
| + | |||
| + | == Unicidad del Límite == |
||
| + | |||
| + | Como se ha dicho en el apartado anterior, si <math>f(x)</math> tiene límite cuando <math>x \to a</math>, este es '''único'''. Es decir: |
||
| + | |||
| + | <math>Si \quad \exists \quad \lim_{ x \to a}f(x)</math> es único. |
||
| + | |||
| + | Como apliación, se puede utilizar para el cálculo de algunos límites, ya que si la función no tiende a un valor único en "a", entonces no existe el límite. |
||
| + | |||
| + | Por ejemplo: |
||
| + | |||
| + | <math>\lim_{x \to 0}\frac{1}{1+e^{\frac{1}{x}}}</math> |
||
| + | |||
| + | Primero realizaremos el límite por la derecha y luego el límite por la izquierda, si son iguales entonces existe el límite: |
||
| + | |||
| + | Por la derecha: |
||
| + | |||
| + | <math>\lim_{x \to 0^{+}}\frac{1}{1+e^{\frac{1}{x}}}=\frac{1}{1+e^{\infty}}=1</math> |
||
| + | |||
| + | Por la izquierda: |
||
| + | |||
| + | <math>\lim_{x \to 0^{-}}\frac{1}{1+e^{\frac{1}{x}}}=\frac{1}{1+e^{-\infty}}=0</math> |
||
| + | |||
| + | Como podemos observar el límite no existe puesto que los dos límites laterales son diferentes. |
||
| + | |||
| + | |||
| + | == Propiedades de las Funciones que tienen límite == |
||
| + | |||
| + | [[Imagen:Graficox-5.jpg|right|thumb|300px|Las dos funciones son idénticas]] |
||
| + | # Si dos funciones <math>f(x)</math> y <math>g(x)</math> tienen idéntico comportamiento en las proximidades de "a" (pero no necesariamente en "a"), entonces las dos tienen el mismo límite cuando <math>x \to a</math>. Es decir: |
||
| + | |||
| + | <math>\lim_{x \to a} f(x)=\lim_{x \to a} g(x) </math> |
||
| + | |||
| + | Por ejemplo tenemos las siguientes funciones: |
||
| + | |||
| + | :<math>f(x)=\frac{x^2+25}{x+5}</math> |
||
| + | :<math>g(x)=x-5</math> |
||
| + | |||
| + | Aunque parezcan iguales no lo son porque para <math>f(x), x=5 \quad \notin dom f</math> y para <math>g(x) x=5 \quad \in dom g </math> |
||
| + | En todos los demás puntos son iguales, entonces aplicando la primera propiedad, tendríamos que el límite es el mismo, apliquemos pues el límite: |
||
| + | |||
| + | <math>\lim_{x \to 5^{-}}\frac{x^2+25}{x+5}=\lim_{x \to 5^{-}}x-5=-10</math> |
||
| + | [[Categoría:Análisis Matemático]] |
||
Revisión del 20:10 8 may 2009
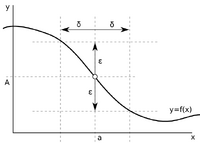
Límite
Siendo una función real de variable real, es decir:
Se dice que tiene límite en "l" cuando , si y sólo si, cuando los valores de "x" se aproximan indefinidamente a "a", los valores de se aproximan indefinidamente a "l".
Simbólicamente:
Es decir, para todo epsilon mayor que 0 existe un delta que depende de epsilon y es mayor que cero, tal que, si los valores de "x" distan de "a" una cantidad menor que delta y son distintos de "a", entonces los correspondientes valores de f(x) distan de "l" una cantidad menor que epsilon.
Si obervamos podemos ver que a "a" no se le exige la condición ya que en los límites sólo se estudia el comportamiento en las proximidades.
Propiedades de los límites
- El límite de una función en un punto si existe , es único y es igual a los límites laterales.
- Si una función tiene limite distinto de cero en un punto entonces existe un entorno del punto en el que los valores que toma f tienen el mismo signo que el límite .
- Si es una constante.
- si
Unicidad del Límite
Como se ha dicho en el apartado anterior, si tiene límite cuando , este es único. Es decir:
es único.
Como apliación, se puede utilizar para el cálculo de algunos límites, ya que si la función no tiende a un valor único en "a", entonces no existe el límite.
Por ejemplo:
Primero realizaremos el límite por la derecha y luego el límite por la izquierda, si son iguales entonces existe el límite:
Por la derecha:
Por la izquierda:
Como podemos observar el límite no existe puesto que los dos límites laterales son diferentes.
Propiedades de las Funciones que tienen límite
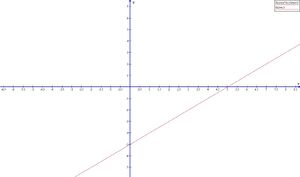
Las dos funciones son idénticas
- Si dos funciones y tienen idéntico comportamiento en las proximidades de "a" (pero no necesariamente en "a"), entonces las dos tienen el mismo límite cuando . Es decir:
Por ejemplo tenemos las siguientes funciones:
Aunque parezcan iguales no lo son porque para y para En todos los demás puntos son iguales, entonces aplicando la primera propiedad, tendríamos que el límite es el mismo, apliquemos pues el límite:
























